前回のコッホ曲線に続きフラクタル図形をpythonで描画。前回の応用で描けそうなシェルピンスキーのギャスケットという図形を描いてみた。
コッホ曲線と同様に図形の一部分にズームしていくと無限に同じ図形が現れる。コッホ曲線は長さが無限大だったが、 シェルピンスキーのギャスケットは無限回計算した際に面積がゼロになる。
塗りつぶされた三角形から各辺の中点を結んでできる三角形を切り取り、辺の長さが半分の3つの三角形に分ける動作を無限に繰り返していく。上図は1回だけ実行したもの。
出力結果
今回は正三角形のみを対象にして一片の長さは可変に出来るようにした。正三角形以外の三角形や回転、他の多角形や立体への拡張も検討するとより面白いかもしれない。
 |
| n=2 |
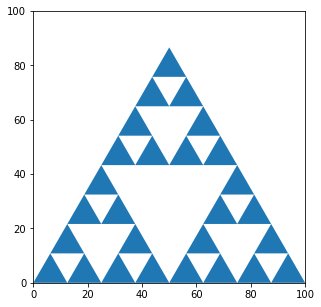 |
| n=3 |
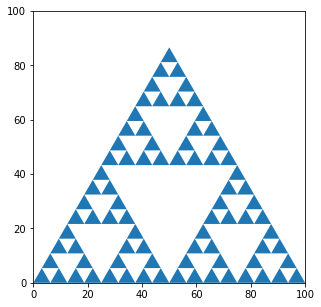 |
| n=4 |
 |
| n=5 |
 |
| n=10 |
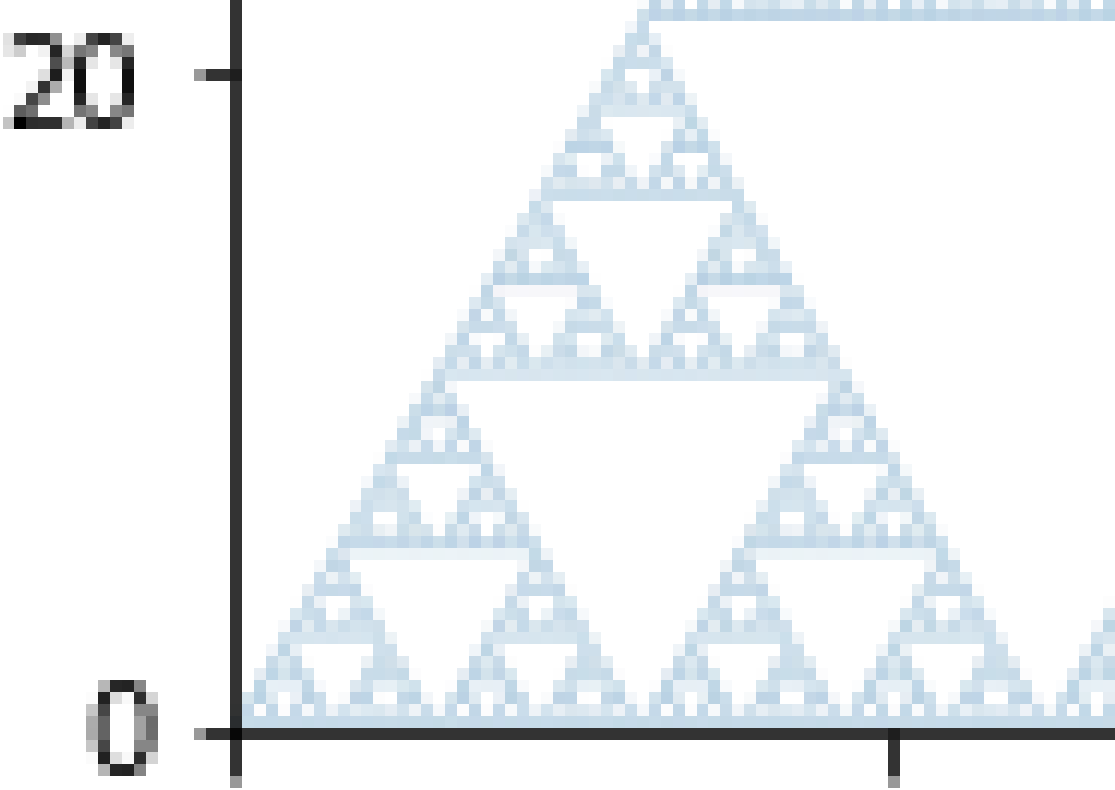 |
| n=10の左下部分拡大 |
n=10の計算は1分以内で出力されはしたが、作成したfigの分解能的に既に表現しきれていない様子。
Pythonコード
今回はMatplotlibのPatchesの使い方を調べはしたが、他のサイトを参考にするのではなくそれなりに一人で作成して描画まで出来た。考え方はコッホ曲線の時と同じく再帰関数を使用したが、描くのは一番小さい三角形のみで良いことに気づいたらとてもシンプルだった。
ハウスドルフ次元について
フラクタル図形についてインターネット検索していると、ハウスドルフ次元というものがあるらしい。Wikipediaを見ても何やら複雑すぎる説明でよくわからないかったが、大阪大学の角教授の資料によると、下記の様に書いてある;
”フラクタル図形の大きさをはかるものとして、t次元ものさし(tは任意の実数)があり、それがちょうどいい具合になるtを図形の「ハウスドルフ次元」とよぶ。”
...
これでも良くわからない。もうちょっと数学をまじめに勉強しておかないとこの手の定義は理解できない。今日はあまり深いこと考えたくないため、また今度読み直すこととする。(これだから何事にも学習が進まない)
参考にしたサイト
- Wikipedia
- フラクタル図形とフラクタル次元
- 大阪大学理学部数学教室、角 大輝教授
- https://www.math.h.kyoto-u.ac.jp/users/sumi/seimeirigaku12talknotree.pdf




