フラクタル図形 ー コッホ曲線をPythonで描く

スマホのニュースで"「複雑系」入門"という本の紹介が掲載されており、コッホ曲線について解説されていた。フラクタル図形はこれまで知らなかった(※1)が、数学で導き出される幾何学的な模様かつ現実にはあり得ないような特徴を持っている（後述のコッホ曲線の長さは無限大！？）ところにとても興味がわいた。

※1 読んですぐは聞いたことあるような、と思ったが、『クレイジーで行こう』の加藤崇さんの会社名がFractaだったのが頭の片隅にあっただけだった。

折角なので自分で描いてみるべく、久しぶりにPythonをさわる。

フラクタルと検索すると決まってロマネスコという野菜の画像が掲載されている。 個人的にあまりなじみがないが、身近にあるフラクタル構造の代表的なモノらしい （画像 from photo AC）

フラクタル図形とは・・・

Wikipediaの定義には以下の様に書かれていたが、いまいち意味が分からない。

• ”フラクタルの特徴は直感的には理解できるものの、数学的に厳密に定義するのは非常に難しい。”　
• ”図形の部分と全体が自己相似（再帰）になっているものなど”

どれだけ拡大していっても無限にディテールが描かれている様な図形が多いっぽい。Wikipediaに載っている例だけでも15個ほどあり、多くの数学者が研究テーマにするほど奥が深い概念らしい。

• カントール集合
• シェルピンスキーのギャスケット
• コッホ曲線
• ペアノ曲線
• 高木曲線
• ヒルベルト曲線
• マンデルブロ集合
• ジュリア集合
• メンガーのスポンジ
• ロマネスコ・ブロッコリー - 明確なフラクタル図形をした野菜。
• バーニングシップ・フラクタル
• リアプノフ・フラクタル
• バーンズリーのシダ

コッホ曲線

フラクタル図形の中でもシンプルなコッホ曲線。直線を三等分した真ん中部分を正三角形に立ち上げる動作を無限に繰り返す。

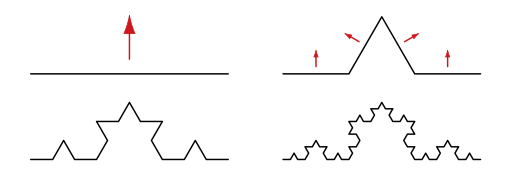Wikipediaより

様々なサイトで既にコードが掲載されているが、一応自分なりに考えて理解しながら進めてみた。一つの”トゲ”を描画する手順は以下：

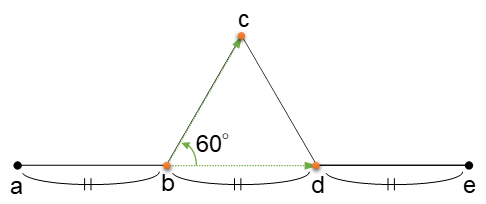
1. 最初の線の両端の座標(a, e)を設定
2. 3等分した2点の座標(b, d)を求める
3. ベクトル(bd)を60度回転させて三角形の頂点(c)を求める
4. 求めた頂点(a, b, c, d, e)をリストに格納

頂点cを求めるのに三角形の高さ（辺x√3/2）を足していく方法で考え始めてしまったが、60度傾くたびに計算がどんどん煩雑になり現実的でない。Wikipediaの説明を全部読めば書いてあったのだが、回転行列で簡単に計算できると気づくまで少々時間がかかった。

import math
import matplotlib.pyplot as plt

# 最初の直線の座標定義
a = (0, 0)
e = (120, 0)

# コッホ曲線の繰り返し回数
n = 20

# 計算結果の保存場所リスト定義（ひとまず最初の点を格納）
result = [a]

# コッホ曲線計算関数を定義
def koch(n, a, e):
    if n == 0:
        return
    
    b = (a[0]+(e[0]-a[0])/3, a[1]+(e[1]-a[1])/3)
    d = (a[0]+2*(e[0]-a[0])/3, a[1]+2*(e[1]-a[1])/3)
    c = (b[0]+(d[0]-b[0])*math.cos(math.radians(60))-(d[1]-b[1])*math.sin(math.radians(60)),
         b[1]+(d[0]-b[0])*math.sin(math.radians(60))+(d[1]-b[1])*math.cos(math.radians(60)))
    
    koch(n-1, a, b)
    result.append(b)
    koch(n-1, b, c)
    result.append(c)
    koch(n-1, c, d)
    result.append(d)
    koch(n-1, d, e)

koch(n, a, e)
result.append(e)

# x座標とy座標のリストを作成
x = [result[i][0] for i in range(len(result))]
y = [result[i][1] for i in range(len(result))]    
plt.plot(x, y)
plt.axis('equal')

再帰関数の考え方に少し混乱したが、ひとまずplot出来るようになった。n=5の時点で既に画面上では変化があまりない。おそらく画像の分解能を上げて作っていけば、ズームをした際に細かいところまで再現されたフラクタル図形が出来るはず。

n=1

n=2

n=3

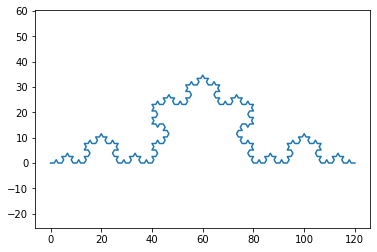n=4

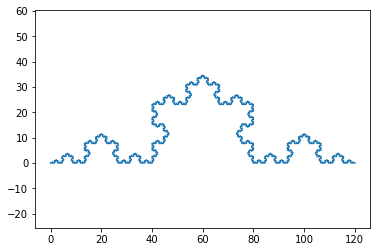n=5

n=10

おそらく他のフラクタル図形でも詳細を描こうとすると意外とPCのパワー・容量を食うことになりそう。コッホ曲線以外も今後気が向いたら試してみたい。

参考にしたサイト

• Kodansha Bluebacks
• 数学の美しき謎…「フラクタル」を形成する「コッホ曲線」には、これほどの「不思議」が詰まっている　（金 重明）
• https://gendai.media/articles/-/110079
• Wikipedia
• https://ja.wikipedia.org/wiki/フラクタル
• https://ja.wikipedia.org/wiki/コッホ曲線
• morikomorou’s blog
• 【python】matplotlibでフラクタル図形(コッホ曲線)を描く
• https://mori-memo.hateblo.jp/entry/2022/02/05/172505
• KIT数学ナビゲーション
• 2次元回転行列の導出
• https://w3e.kanazawa-it.ac.jp/math/category/gyouretu/senkeidaisu/henkan-tex.cgi?target=/math/category/gyouretu/senkeidaisu/rotation_matrix_2d.html